GC Insights: Identifying conditions that sculpted bedforms – human insights to building an effective AI (artificial intelligence)

Insights from a geoscience communication activity, verified using preliminary investigations with an artificial neural network, illustrate that observation of humans' abilities can help design an effective artificial intelligence or “AI”. Even given only one set of “training” examples, survey participants could visually recognize which flow conditions created bedforms (e.g. sand dunes and riverbed ripples) from their shapes, but an interpreter's geoscience expertise does not help. Together, these observations were interpreted as indicating that a machine learning algorithm might be trained successfully from limited data, particularly if it is “helped” by pre-processing bedforms into a simple shape familiar from childhood play.

1 Introduction

Environmental flows shape the surface they flow over. The variety of features produced (e.g. sand ripples on a beach), known as bedforms, reflect and preserve characteristics (e.g. speed and depth) of the flowing ice, water or air (Venditti, 2012; Bullard et al., 2011; Storrar and Stokes, 2007). The relationships between bedform morphology and flow are contested where observation is extremely difficult, such as under ice sheets (e.g. Hillier et al., 2018; King et al., 2009), and best understood for unidirectional water flow over sand in a laboratory setting, mimicking a river. Even in this idealized fluvial setting, it is difficult to construct a one-to-one link between bedform type (e.g. ripples or dunes) and specific flow conditions (Venditti, 2012; Froehlich, 2020). Illustratively, ripples have a higher aspect ratio (height $/$ length) than dunes (e.g. Allen, 1968), yet the observational ranges overlap (Venditti, 2012), creating uncertainty when attempting to link morphology with hydraulic conditions. Many variables related to hydraulics and/or the physics of sediment movement have been proposed to remove the overlap in bedform stability diagrams such as Fig. 1a. Only recently has a distinct and non-overlapping zonation of bedform type and flow-sediment condition been developed using a quantity called shear velocity (Duran Vinet et al., 2019). Inverting this result may help realize the aspiration of developing a means to reliably infer flow conditions from bedform morphology, which is often the only option for inferring past environmental conditions on Earth (Leary and Ganti, 2020) or Mars (Ohata et al., 2017; Edgett and Lancaster, 1993).

Machine learning or “AI” (artificial intelligence) algorithms, such as artificial neural networks (ANNs), have great potential in geomorphology (Sofia et al., 2016; Froehlich, 2020; Valentine and Kalnins, 2016; Shumack et al., 2020) and offer an opportunity to examine this problem, as they do not assume simple (e.g. linear or one-to-one) relationships between inputs and predicted variables (Wang et al., 2009; Faruk, 2010). Unexploited morphological subtleties may exist by which to categorize bedforms or even to accurately position them on stability diagrams. This work examines the scope for using ANNs to distinguish the flow conditions in which bedforms originated by asking if the ability exists in non-artificial (human) intelligence for two particulars:

• Q1.

  Is it possible to identify the environment (e.g. river and desert) of a bedform's genesis from its shape?

• Q2.

  In the fluvial environment, is it possible to distinguish flow conditions?

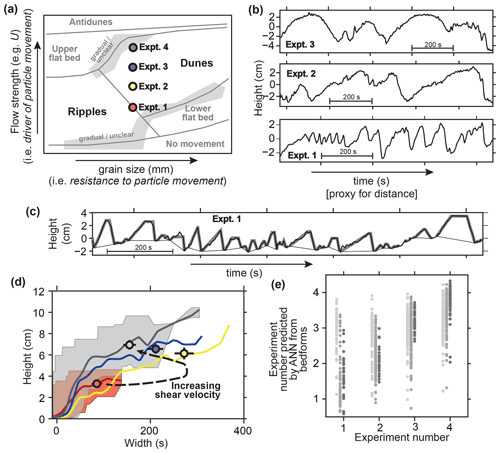
Figure 1 (a) Illustrative bedform stability “phase diagram” for unidirectional fluvial (i.e. river) bedforms, synthesized from multiple sources (Ohata et al., 2017; Lewis and McConchie, 1994; Southard and Boguchwal, 1990). Main types considered here (i.e. ripples and dunes) are highlighted. Experiments (Expts.) 1–4 are positioned indicatively. (b) Distance–height profiles (strictly speaking time series) like those given unannotated to participants, i.e. one each from Expts. 1–3, all scaled to the same dimensions. Horizontal axis is time because in the flume tank a stationary sensor recorded height as bedforms passed beneath it. (c) Example of how height (H) and width (W) are determined. Measured heights (thick black line) are processed using the SWT algorithm to identify bedforms, drawing a line beneath them (thin black line), which is then approximated as flat-topped cones (grey lines). SWT parameters as in Hillier (2008). (d) Height–width relationships for the four experiments, with colours as in (a): lines are sliding means with W (Gaussian weights, width 60 s); shaded areas are full ranges for Expts. 1 and 4; and dots are the means (± 2σ) of the upper quartile of the data when the small bedforms (i.e.H< 0.5 cm) are excluded. (e) Comparison of the actual experiment number with out of sample prediction of the experiment number by the ANN using H and W: individual bedforms (light grey) and subsets of five bedforms with (grey) and excluding (dark grey) small bedforms.

2 Method, data and ethics

An online survey was conducted, initially at the “Non-Equilibrium Flow and Landform Coupling Workshop” (19 May 2021) and then expanded to participants without geomorphological expertise using authors' close contacts (friends, colleagues and family). For Q1, participants attributed distance–height profiles across 34 individual bedforms and 13 bedform sequences (≥3 bedforms) to one of four environments (fluvial (river), glacial, marine and aeolian (desert)). For Q2, participants ranked three profiles according to flow strength (shear velocity), thrice for individual forms and thrice for bedform sequences. Examples were provided to isolate visual shape analysis from prior knowledge (Fig. 1b); black-and-white profiles were used to exclude contextual clues (dataset characteristics and other features in the landscape), and the order of options (e.g. B, A and C) was shuffled for each participant to prevent bias. Scale (e.g. metres) readily distinguishes the environment without using bedform shape, so it was not given.

Ethical approval was given by the Ethics Review Sub-Committee at Loughborough University.

Aeolian data are from ASTER (v2; Advanced Spaceborne Thermal Emission and Reflection Radiometer) across linear and transverse dune types from the Namib Desert (Bullard et al., 2011); glacial data are from near Lough Gara in Ireland (Hillier and Smith, 2008); fluvial data are from four laboratory experiments (Expts. 1–4) of non-linearly increasing shear velocity (Unsworth, 2015); and marine data are from the Irish Sea. Distance–height profiles of these data were created, although for the fluvial measurements “time” was used as a proxy for “distance” (see Fig. 1b). For the survey, representative examples of individual bedforms and sequences were manually selected from these datasets. Pre-processing to estimate bedforms' height (H) and width (W) – see Fig. 1c and d – used the spatial wavelet transform (SWT) algorithm (Hillier, 2008) and fitting of flat-topped cones (Hillier, 2006).

ANN analysis to follow up the survey used a multi-layered perceptron (MLP) with four hidden layers with 28, 56, 56 and 28 nodes, each with a ReLU (rectified linear unit) activation function. In a baseline analysis, input to predict the fluvial flow regime (coded by experiment number) was non-overlapping profile segments 160 s long. After this, to “help” the ANN bedform, shapes (H and W) were input once each per analysis, either (i) individually or (ii) as pseudo-sequences – groups of five bedforms in increasing size order, selected at random without replacement. Weights and biases were updated using the Adam optimizer of PyTorch using a loss function that calculates the mean squared error, all within a feed-forward back-propagation algorithm.

3 Results

Of the 42 survey participants 25 self-identified as geoscientists, and 16 did not. For Q1, participants correctly identified the one of four environments (e.g. fluvial and aeolian) in which individual features originated 32 % of the time, slightly if significantly (two-tailed t test, p≪ 0.01) better than the 25 % expected of guesswork. This rises to 51 % for bedform sequences. For Q2, participants ranked entirely correctly three flow strengths (Expts. 1–3) for 46 % of individual features and 60 % of sequences, much better than the 16 % expected of guesswork (p≪ 0.01).

In none of the questions did geoscientists perform better than non-geoscientists, with mean percentages of correct answers being indistinguishable (two-tailed t test, p> 0.05). The overall sentiment is encapsulated by one comment:

I felt this was a geometrical exercise of recognizing same patterns at different scales. I did not feel that my experience as an “expert” in bedforms really made any difference from, say, my son taking the test.

Several participants commented that their ability to distinguish environments might be to do with characteristics of the data (e.g. smoothness due to data resolution), not bedform shape. This is a potential pitfall of training an ANN, avoided here by only analysing the fluvial data.

In the baseline ANN analysis, flow regime was predicted poorly (r²=0.03). Fitting a simplified geometry (H and W) to bedforms improves results dramatically, particularly if pseudo-sequences of bedforms are used (Fig. 1e); individual forms are weakly predictive (light grey, r²=0.11), but sub-sets of five bedforms are more strongly so (grey, r²=0.56), particularly if very small bedforms present in all experiments (H< 0.5 cm) are excluded (dark grey, r²=0.80). This is consistent with a visual assessment (Fig. 1d) where individual morphologies overlap between experiments, but their trends, as well as averages over a number of bedforms, are distinctly different.

4 Discussion

Morphologies from differing environments (e.g. glacial and fluvial) can be viewed as similar, indicators of analogous processes at work (e.g. Shaw, 1983) and modelled with identical equations (e.g. Fowler, 2002; Duran Vinet et al., 2019) or statistics (e.g. Hillier et al., 2016; Einstein, 1937). Despite similarities in appearance, the survey results clearly demonstrate a level of ability to distinguish flow conditions from distance–height data of the bed and, unsurprisingly, imply that an ANN should perform better if utilizing sequences of bedforms rather than evaluating individual forms in isolation. Interestingly, geoscientists' a priori and contextual knowledge added little, indicating that all required visual cues lie within the distance–height profiles. Furthermore, one training dataset sufficed for the survey's participants, a stark contrast to the thousands of datasets required to train ANNs performing pure pattern recognition (e.g. Bishop, 1996), suggesting that participants drew on significant previous learning (e.g. identification of basic idealized shapes). Together, these observations prompt the testable idea that an effective ANN might be efficiently trained by helping it via pre-processing profiles into simple shape parameters that would have been readily understood by all participants (H and W).

Preliminary analysis with an ANN supports our speculations. It demonstrates that an AI with predictive efficacy can be built using limited data, improved by using bedform sequences (Fig. 1e). The increase in predictive skill to 0.80 with pre-processing help demonstrates, in principle, the utility of this approach when building an effective AI for geomorphology that avoids the crippling need for thousands of datasets when examples in nature are often limited in number. Speculatively, it follows that machine learning techniques might work well and be trained efficiently wherever non-experts make good decisions based on images. This study was on equilibrium conditions but illustrates that ANNs may be key to linking forms and flow for transitional, non-equilibrium conditions (e.g. Myrow et al., 2018).